AVL Tree

AVL Tree

AVL Tree yang dinamakan dari pembuatnya yaitu Adelson-Velsky and Landis’ tree, adalah self-balancing binary search tree. Dalam AVL Tree, ketinggian anak anak di setiap simpul berbeda paling banyak 1. Kapan saja jika perbedaan ketinggian menjadi lebih besar dari 1 maka penyeimbangan pohon dilakukan untuk memulihkan propertinya.

dalam AVL Tree ada 2 basic operation yaitu Right Rotation and Left Rotation.

Cara Rotasi ini berfungsi untuk menyeimbangkan Tree:

1. Biarkan  node A menjadi node baru yang di add ke tree.
2. Setelah node A di add, dari node A ke root untuk menemukan node yang tidak seimbang.
3. apabila ketemu node yang tidak seimbang maka akan diseimbangkan dan terus mengecek apabila masih ada node pada tree yang tidak seimbang.

Jka Anda telah menemukan simpul z yang tidak seimbang, Node y adalah anak dari z dan x menjadi cucu dari z maka akan ada empat kemungkinan, yaitu 

• Case Left - Left: - x adalah left child dari node y dan y adalah left child dari node z.

• Case Left - Right: - x adalah right child dari node y dan y adalah left child dari node z.

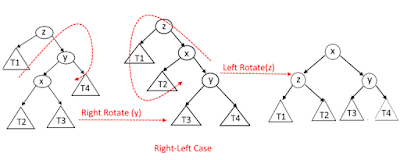
• Case Right - Left: - x adalah left child dari node y dan y adalah right child dari node z.

• Kasus Right - Right: - x adalah right child dari node y dan y adalah right child dari node z.

Operasi Insertion:

• Insert node baru menggunakan rekursi agar saat melacak kembali Anda akan men-check semua parent node untuk memeriksa apakah mereka masih seimbang atau tidak.
• Setiap node memiliki height dengan nilai default sebagai 1.
• Ketika node baru ditambahkan, height dari parent node akan bertambah 1.
• Jadi seperti yang disebutkan pada langkah 1, setiap height dari ancestors nya akan diperbarui saat kembali melacak dari atas sampai ke root.
• Di setiap node, Balance Factor juga akan diperiksa. faktor keseimbangan = (height left tree - height right tree).
• Jika Balance Factor = 1 berarti tree sudah seimbang pada node tersebut.
• Jika Balance Factor > 1 berarti tree tidak seimbang pada node tersebut, height left tree lebih tinggi daripada height right tree sehingga itu berarti kita perlu rotasi. (Baik Left - Left atau Left - Right).
• Jika node saat ini yang kita periksa adalah X dan Jika node baru kurang dari X.left maka itu akan menjadi case Left - Left, dan jika node baru lebih besar dari X.left maka itu akan menjadi Case Left - Right. 
• Jika Balance Factor < -1 berarti tree tidak seimbang pada node tersebut, height right tree lebih tinggi dari height left tree sehingga itu berarti kita perlu rotasi. (Baik Case Right - Right atau RIght - Left)
• Katakanlah node saat ini yang kita periksa adalah X dan Jika node baru kurang dari X.right maka itu akan menjadi Case Right - Right, dan jika node baru lebih besar dari X.right maka itu akan menjadi Case Right - Left.